西瓜书5 神经网络

5、神经网络

神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”。

5.1 神经元模型

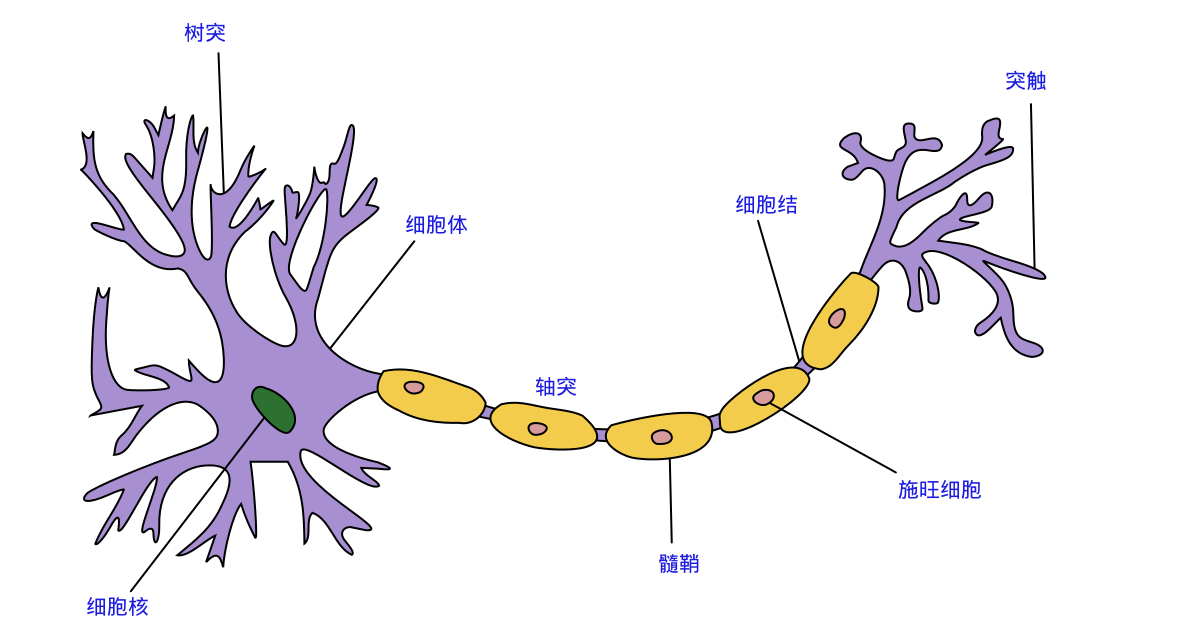
神经网络中最基本的单元是神经元模型（neuron）。在生物神经网络的原始机制中，每个神经元通常都有多个树突（dendrite），一个轴突（axon）和一个细胞体（cell body），树突短而多分支，轴突长而只有一个；
在功能上，树突用于传入其它神经元传递的神经冲动，而轴突用于将神经冲动传出到其它神经元，当树突或细胞体传入的神经冲动使得神经元兴奋时，该神经元就会通过轴突向其它神经元传递兴奋。

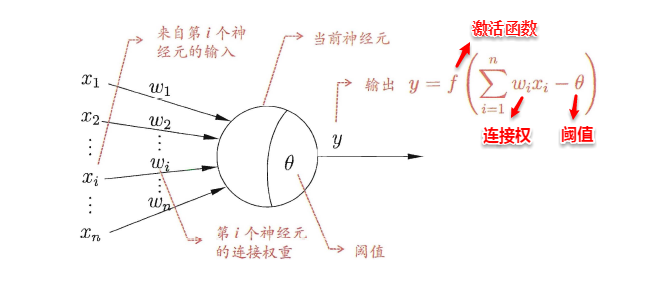
“M-P 神经元模型”（McCulloch-Pitts Neuron）是对生物神经元的数学抽象，也称为阈值逻辑单元。其工作原理如下：

输入：多个输入信号通过带权重的连接（connection weight）传递到神经元。
处理：
1. 计算所有输入的加权和（总输入值）。
2. 将加权和与该神经元的阈值（threshold）相减。
3. 通过激活函数（activation function）处理差值，生成输出。
输出：通过轴突传递给其他神经元。

Pasted image 20250324182656.png

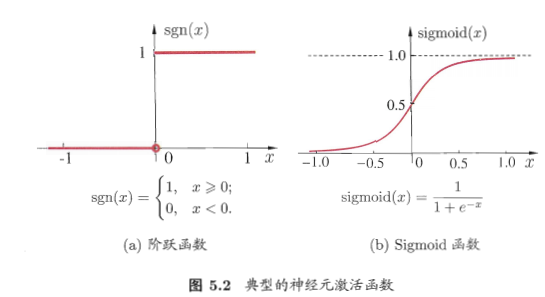
与线性分类十分相似，神经元模型最理想的激活函数也是阶跃函数，即将神经元输入值与阈值的差值映射为输出值1或0，若差值大于零输出1，对应兴奋；若差值小于零则输出0，对应抑制。但阶跃函数不连续，不光滑，故在M-P神经元模型中，也采用Sigmoid函数来近似， Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内，所以也称为挤压函数（squashing function）。

Pasted image 20250324182800.png

将多个神经元按一定的层次结构连接起来，就得到了神经网络。它是一种包含多个参数的模型，比方说10个神经元两两连接，则有100个参数需要学习（每个神经元有9个连接权以及1个阈值），若将每个神经元都看作一个函数，则整个神经网络就是由这些函数相互嵌套而成。

5.2 感知机与多层网络

感知机（Perceptron）是由两层神经元组成的一个简单模型

只有输出层是M-P神经元，即只有输出层神经元进行激活函数处理，也称为功能神经元（functional neuron）；
输入层只是接受外界信号（样本属性）并传递给输出层（输入层的神经元个数等于样本的属性数目），而没有激活函数。
这样一来，感知机与之前线性模型中的对数几率回归的思想基本是一样的，都是通过对属性加权与另一个常数求和，再使用sigmoid函数将这个输出值压缩到0-1之间，从而解决分类问题。不同的是感知机的输出层应该可以有多个神经元，从而可以实现多分类问题，同时两个模型所用的参数估计方法十分不同。西瓜书3 线性模型#3.2 线性几率回归

给定训练集，则感知机的 $n + 1$ 个参数（n个权重+1个阈值）都可以通过学习得到。阈值θ可以看作一个输入值固定为-1的哑结点的权重ωn+1。

哑节点📔

为了统一权重和阈值，感知机引入了一个巧妙的技巧：哑结点。具体做法是：

在输入层增加一个额外的“输入”，记作 $x_{n + 1}$ 。
这个输入的值固定为 $- 1$ ，也就是 $x_{n + 1} = - 1$ ，不会随着样本变化。
为这个额外的输入分配一个权重，记作 $w_{n + 1}$ 。
特别地，我们让 $w_{n + 1} = θ$ ，也就是说，这个新权重的值就是原来的阈值。
现在，输入变成了 $x_{1}, x_{2}, \dots, x_{n}, x_{n + 1}$ ，对应的权重是 $w_{1}, w_{2}, \dots, w_{n}, w_{n + 1}$ 。总共有 $n + 1$ 个输入和 $n + 1$ 个权重。
通过引入哑结点，原来的 $n$ 个权重和 1 个阈值变成了 $n + 1$ 个权重（ $w_{1}, w_{2}, \dots, w_{n}, w_{n + 1}$ ）。这样，所有的参数都变成了“权重”，可以用相同的规则来更新。

感知机的学习规则是：

$w_{i} \leftarrow w_{i} + η (y - \hat{y}) x_{i}$ for $i = 1, 2, \dots, n + 1$

其中：

$η$ 是学习率，控制调整步长。
$y$ 是真实标签。
$\hat{y}$ 是感知机的预测输出。
$x_{i}$ 是输入值（特别地， $x_{n + 1} = - 1$ ）。
对于哑结点，更新时：

$x_{n + 1} = - 1$ ， $w_{n + 1}$ 也会根据这个规则调整，实际上就是在调整原来的阈值 $θ$ 。

感知机权重的学习规则(当激活函数为阶跃函数时)
对于每个训练样本 ( $x$ , $y$ )：
计算预测输出 $\hat{y} = f (\sum_{i = 1}^{n + 1} w_{i} x_{i})$ 。
检查预测是否正确：
如果 $\hat{y} = y$ ，不调整权重。
如果 $\hat{y} \neq y$ ，更新权重：
$w_{i} \leftarrow w_{i} + η (y - \hat{y}) x_{i}$ for $i = 1, 2, \dots, n + 1$
重复此过程，直到所有样本都被正确分类或达到最大迭代次数。

推导💡

预测值定义
对于样本 $(x, y)$ ，其预测值表达式为：

y^{'} = f (\sum_{i = 1}^{n} ω_{i} x_{i} - θ) = f (\sum_{i = 1}^{n + 1} ω_{i} x_{i})

其中 $x_{i + 1} = - 1$ 为固定输入值

误差函数
定义均方误差：

E = \frac{1}{2} (y - y^{'})^{2}

梯度下降过程
通过求偏导数计算权重更新量：

\frac{\partial E}{\partial ω_{i}} = - (y - y^{'}) \cdot \frac{\partial f (\sum_{i = 1}^{n + 1} ω_{i} x_{i})}{\partial ω_{i}}

阶跃函数特性
当激活函数 $f$ 为阶跃函数时：

\frac{\partial f}{\partial ω_{i}} = x_{i}

权重更新公式
设定学习率 $η \in (0, 1)$ ，得到权重调整规则：

Δ ω_{i} = η (y - y^{'}) x_{i}

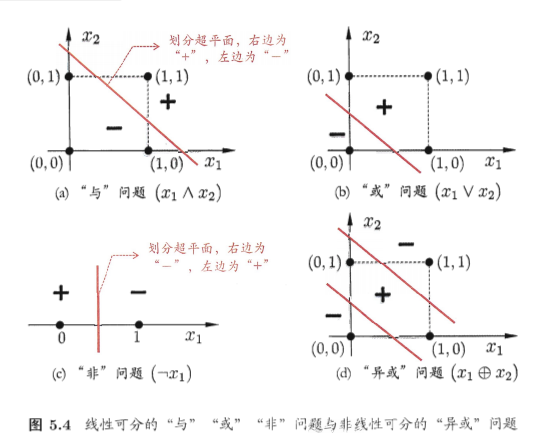
由于感知机模型只有一层功能神经元，因此其功能十分有限，只能处理线性可分的问题，对于这类问题，感知机的学习过程一定会收敛（converge），因此总是可以求出适当的权值。而求得适当的权向量w=(wi;w2;…;wn+1);否则感知机学习过程将会发生振荡(fluctuation),w 难以稳定下来，不能求得合适解，例如感知机甚至不能解决如图5.4(d)所示的异或这样简单的非线性可分问题(.异或问题)，需要考虑使用多层功能神经元，即神经网络。
Pasted image 20250324190759.png

在神经网络中，输入层与输出层之间的层称为隐含层或隐层（hidden layer），隐层和输出层的神经元都是具有激活函数的功能神经元。只需包含一个隐层便可以称为多层神经网络，常用的神经网络称为“多层前馈神经网络”（multi-layer feedforward neural network），该结构满足以下几个特点：

每层神经元与下一层神经元之间完全互连
神经元之间不存在同层连接
神经元之间不存在跨层连接

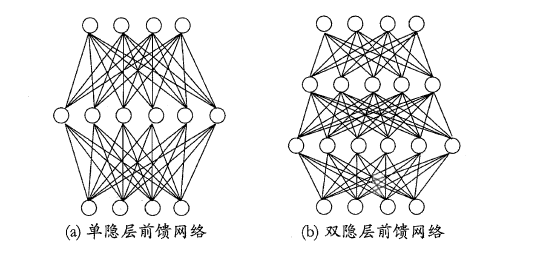
根据上面的特点可以得知：这里的“前馈”指的是网络拓扑结构中不存在环或回路，而不是指该网络只能向前传播而不能向后传播（下节中的BP神经网络正是基于前馈神经网络而增加了反馈调节机制）。神经网络的学习过程就是根据训练数据来调整神经元之间的“连接权”以及每个神经元的阈值，换句话说：神经网络所学习到的东西都蕴含在网络的连接权与阈值中。

5.3 BP神经网络算法

BP神经网络算法即误差逆传播算法（error BackPropagation）是为学习多层前馈神经网络而设计，BP神经网络算法是迄今为止最成功的的神经网络学习算法。

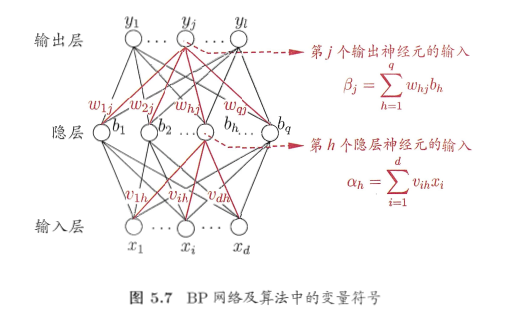
Pasted image 20250324192644.png

BP神经网络算法也使用梯度下降法（gradient descent），以单个样本的均方误差的负梯度方向对权重进行调节。
BP算法首先将误差反向传播给隐层神经元，调节隐层到输出层的连接权重与输出层神经元的阈值；
接着根据隐含层神经元的均方误差，来调节输入层到隐含层的连接权值与隐含层神经元的阈值。

#待补充

BP算法的更新规则是基于每个样本的预测值与真实类标的均方误差来进行权值调节，即BP算法每次更新只针对于单个样例。需要注意的是：BP算法的最终目标是要最小化整个训练集D上的累积误差，即：

E = \frac{1}{m} \sum_{k = 1}^{m} E_{k}

如果基于累积误差最小化的更新规则，则得到了累积误差逆传播算法（accumulated error backpropagation），即每次读取全部的数据集一遍，进行一轮学习，从而基于当前的累积误差进行权值调整。
一般来说，标准BP算法每次更新只针对单个样例，参数更新得非常频繁，而且对不同样例进行更新的效果可能出现“抵消”现象。因此，为了达到同样的累积误差极小点，标准BP算法往往需进行更多次数的迭代。累积BP算法直接针对累积误差最小化，它在读取整个训练集D一遍后才对参数进行更新，其参数更新的频率低得多。但在很多任务中，累积误差下降到一定程度之后，进一步下降会非常缓慢，这时标准BP往往会更快获得较好的解，尤其是在训练集D非常大时更明显。
Horniketal.证明，只需一个包含足够多神经元的隐层，多层前馈网络就能以任意精度逼近任意复杂度的连续函数。然而，如何设置隐层神经元的个数仍是个未决问题，实际应用中通常靠“试错法”（trial-by-error）调整。

BP神经网络强大的学习能力常常容易造成过拟合问题，有以下两种策略来缓解BP网络的过拟合问题：

早停：将数据分为训练集与测试集，训练集用于学习，测试集用于评估性能，若在训练过程中，训练集的累积误差降低，而测试集的累积误差升高，则停止训练。
引入正则化（regularization）：基本思想是在累积误差函数中增加一个用于描述网络复杂度的部分，例如所有权值与阈值的平方和，其中λ∈（0,1）用于对累积经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。

E = λ \frac{1}{m} \sum_{k = 1}^{m} E_{k} + (1 - λ) \sum_{i} w_{i}^{2}

5.4 全局最小与局部最小

局部极小（local minimum）和全局最小（global minimum）

局部极小解：参数空间中的某个点，其邻域点的误差函数值均不小于该点的误差函数值。
全局最小解：参数空间中的某个点，所有其他点的误差函数值均不小于该点的误差函数值。

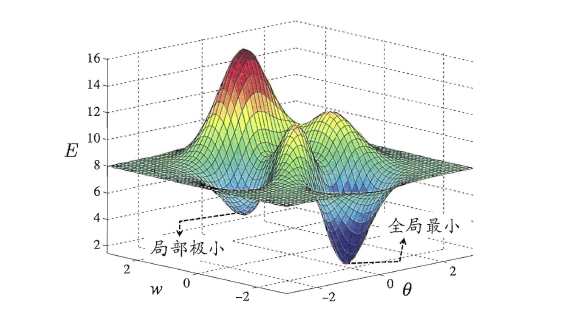
要成为局部极小点，只要满足该点在参数空间中的梯度为零。局部极小可以有多个，而全局最小只有一个。全局最小一定是局部极小，但局部最小却不一定是全局最小。通常使用以下策略尽可能地去接近全局最小。

以多组不同参数值初始化多个神经网络，按标准方法训练，迭代停止后，取其中误差最小的解作为最终参数。这样就可能陷入不同的局部极小，从中进行选择有可能获得更接近全局最小的结果。
使用“模拟退火”(simulated annealing) 技术，模拟退火在每一步都以一定的概率接受比当前解更差的结果，从而有助于“跳出”局部极小。在每步迭代过程中，接受“次优解”的概率要随着时间的推移而逐渐降低，从而保证算法稳定。
使用随机梯度下降，即在计算梯度时加入了随机因素，使得在局部最小时，计算的梯度仍可能不为0，从而迭代可以继续进行。

5.5 其他常见神经网络

RBF（径向基函数）网络
ART（自适应谐振理论）网络
SOM（自组织映射）网络
级联相关网络
Elman网络（递归神经网络之一）
Boltzman机
#待补充

5.6 深度学习

理论上，参数越多，模型复杂度就越高，容量（capability）就越大，从而能完成更复杂的学习任务。深度学习（deep learning）正是一种极其复杂而强大的模型。

怎么增大模型复杂度呢？两个办法，一是增加隐层的数目，二是增加隐层神经元的数目。前者更有效一些，因为它不仅增加了功能神经元的数量，还增加了激活函数嵌套的层数。但是对于多隐层神经网络，经典算法如标准BP算法往往会在误差逆传播时发散（diverge），无法收敛达到稳定状态。

那要怎么有效地训练多隐层神经网络呢？一般来说有以下两种方法：

无监督逐层训练（unsupervised layer-wise training）：每次训练一层隐节点，把上一层隐节点的输出当作输入来训练，本层隐结点训练好后，输出再作为下一层的输入来训练，这称为预训练（pre-training）。全部预训练完成后，再对整个网络进行微调（fine-tuning）训练。一个典型例子就是深度信念网络（deep belief network，简称DBN）。这种做法其实可以视为把大量的参数进行分组，先找出每组较好的设置，再基于这些局部最优的结果来训练全局最优。
权共享（weight sharing）：令同一层神经元使用完全相同的连接权，典型的例子是卷积神经网络（Convolutional Neural Network，简称CNN）。这样做可以大大减少需要训练的参数数目。

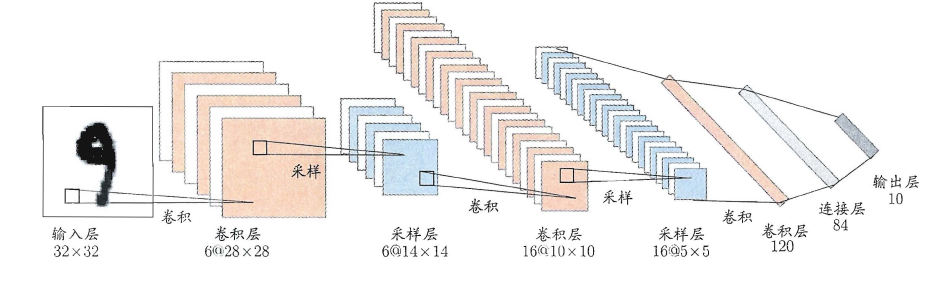
深度学习可以理解为一种特征学习（feature learning）或者表示学习（representation learning），无论是DBN还是CNN，都是通过多个隐层来把与输出目标联系不大的初始输入转化为与输出目标更加密切的表示，使原来只通过单层映射难以完成的任务变为可能。即通过多层处理，逐渐将初始的“低层”特征表示转化为“高层”特征表示，从而使得最后可以用简单的模型来完成复杂的学习任务。

传统任务中，样本的特征需要人类专家来设计，这称为特征工程（feature engineering）。特征好坏对泛化性能有至关重要的影响。而深度学习为全自动数据分析带来了可能，可以自动产生更好的特征。